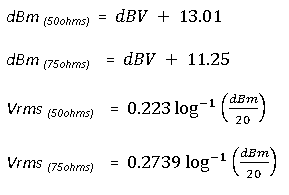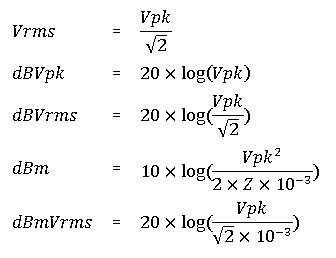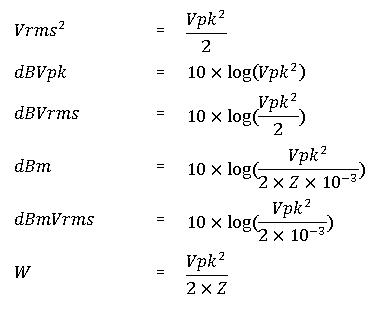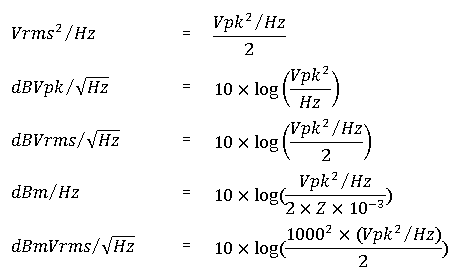Useful Formulas, Conversions, and Reference Information
This topic contains basic Voltage/Power conversion formulas and summary tables that are useful for converting and/or calculating the various VSA signal analysis measurement data results.
Quick Reference Tables
Decibel To Voltage Power Reference Table| dBm deciBels referenced to a milliWatt: dB relative to 1 milliwatt dissipated in the nominal input impedance of the analyzer (50ohms) | dBVrms | dBVpk | Vrms | Vpk |
|---|---|---|---|---|
|
20.0 |
6.99 |
10 |
2.24 |
3.162 |
|
13.0 |
0 |
3 |
1.00 |
1.414 |
|
10.0 |
-3.01 |
0 |
0 .707 |
1.0 |
|
3.0 |
-10 |
- 7 |
0.316 |
0 .447 |
|
0.0 |
-13.01 |
-10 |
0.224 |
0.316 |
|
- 7.0 |
-20 |
-17 |
0.01 |
0.1414 |
|
-10.0 |
-23.01 |
-20 |
0.0707 |
0.1 |
|
-20.0 |
-33.01 |
-30 |
0.0224 |
0.0316 |
Power Ratio (dB) Reference Table| Voltage Ratio |
Power Ratio (v2/v1) |
Decibels (P2/P1) |
|---|---|---|
|
1 |
1 |
0 dB |
|
1.414 |
2 |
3 dB |
|
2 |
4 |
6 dB |
|
3.16 |
10 |
10 dB |
|
10 |
100 |
20 dB |
Useful Equations
Common power and conversion equations used to derive the various trace data results.
Concepts
Understanding Decibels
The decibel is a logarithmic ratio of power or voltage. Because of this, the following is true:
- 0 dB is a ratio of 1 (voltage and power).
- 3 dB is a power ratio of 2.
- 6 dB is a voltage ratio of 2.
- Inverting a ratio changes sign of decibel value (ratio of 2 is 3 dB; 1/2 is -3 dB).
- 10 dB is a power ratio of 10 (the only point where the decibel value and the ratio value are the same for power).
- As a number increases by a factor of 10, the decibel value increases by 10 for power ratios and 20 for voltage ratios.
The decibel is sometimes used to express electrical quantities in a convenient form. The definition of the decibel is based on the ratio of two power levels (log indicates the base ten logarithm):
dB = 10 log (P2/P1)
The decibel equation can be modified to express the decibel as a ratio of two voltage levels:
P2 = (V^2/R2)
P1 = (V^2/R1)
dB = 10 log ((V2^2/R2)/(V1^2/R1))
And, if R1 = R2 (the resistances are the same):
dB = 10 log (V2/V1)^2
dB = 20 log (V2/V1)
Strictly speaking, the voltage equation is valid only if the two resistances are the same. For instance, if the input voltage and the output voltage of an amplifier were being compared and the input resistance and output resistance are different, they must be accounted for when calculating decibels. In practice, however, this is often ignored. For example, in operational amplifier circuits, the input impedance is very large while the output impedance is quite small. Usually, the important parameter in this type of circuit is voltage gain (not power gain). In this type of system, the decibel equation for voltage is used almost exclusively.
Decibels compress widely varying electrical values onto a more manageable logarithmic scale. For example, the range of powers from 100 watts to 1 microwatt is a ratio of 10,000,000 but is expressed in decibels as only 80 dB.
