Custom FM Chirp Example

If using the WobbulatingChirp.pbp or DualRateChirp.pbp setting files in this example, with a system using an external or wideband I/Q configuration, you may have to adjust the Sample Clock Rate, Modulation Bandwidth, Arb Voltage and Arb Filter parameters.

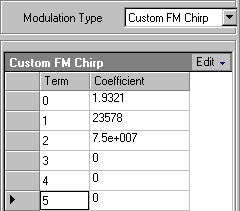
The N7620B Signal Studio for Pulse Building software provides Custom FM Chirp modulation, generated by using a polynomial. The polynomial represents the instantaneous frequency verses time. Polynomial coefficients are entered into a table on the Custom FM chirp panel to create the frequency pattern. Data entry into the GUI is shown here. Use the right mouse button to add or delete coefficients from the list.

The formula shown below is used to generate the coefficients.

Assuming that the Custom FM signal is defined by

sin( f(t))

and

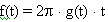
where g(t) is the instantaneous frequency verses time. g(t) can be approximated using a polynomial.

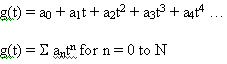
where a₀, a₁, a₂, a₃, a₄ … are the coefficients provided by the user.

The simplest case is where the instantaneous frequency is constant and just provides a frequency offset to the pulse.

It can be represented as

the coefficients are

[ f_c, 0, 0, 0, 0, …]

A linear chirp is defined by

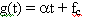
where 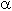is the frequency rate of change and f_c is a constant offset. The polynomial representation of this is

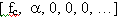
The trailing coefficients of zero are assumed and do not have to be entered by the user.

Almost any frequency pattern can be generated with this technique so long as the physical limits of the hardware are not exceeded. Here are two examples of Custom FM (non-linear) chirps. The frequency patterns were designed using MatLab and compared to a linear chirp. The MatLab scripts used to generate the non-linear chirp coefficients can be found at the end of this section.

The linear chirp has the following characteristics:

Arb Sample Rate = 100 MHz
PRI = 100 us
Pulse Width = 10 us
Rise Time = 30 ns
Fall Time = 30 ns
Peak Deviation = 10 MHz
Chirp Rate = 20MHz/10us

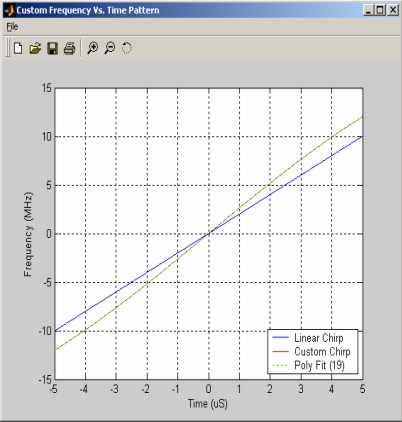
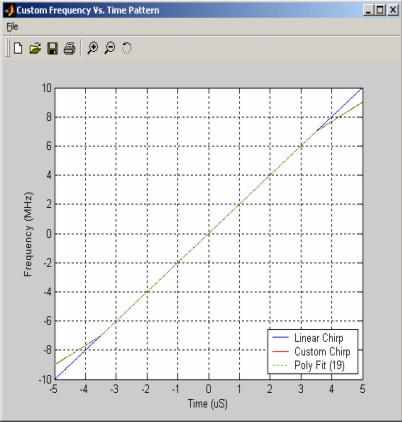
The first custom chirp is very similar to the linear chirp except that a sinusoidal wobbulation has been added to its frequency pattern. The red trace is the desired frequency pattern and the green trace is derived using 19 polynomial coefficients.

Figure 1 - Frequency Pattern of Custom Chirp #1

The spectrum generated by this custom frequency pattern is shown in figure 2.

Figure 2 - Spectrum of Custom Chirp #1

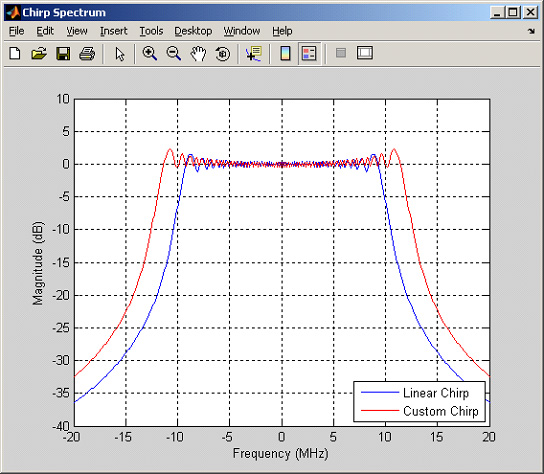
It is important to note that the spectrum of custom chirp #1 occupies approximately the same bandwidth as the linear chirp. This bandwidth matching is mostly a result of the two frequency patterns being very similar. The signal bandwidth increases significantly when the amplitude of the sinusoidal wobbulation is increased or as the custom pattern deviates from the linear chirp.

The second custom chirp consists of a frequency pattern with two different linear slopes. The frequency change is slower at the beginning and the end of the pattern as compared to the middle. Figure 3 shows the frequency pattern.

Figure 3 - Frequency Pattern of Custom Chirp #2

The spectrum generated by this custom frequency pattern is shown in figure 4.

Figure 4 - Spectrum of Custom Chirp #2

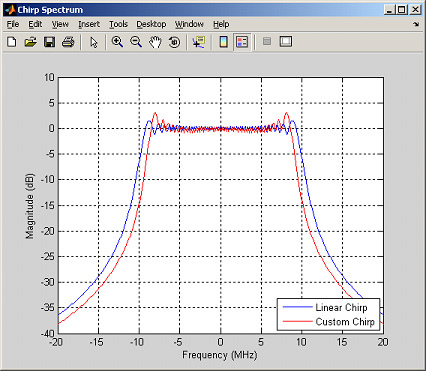
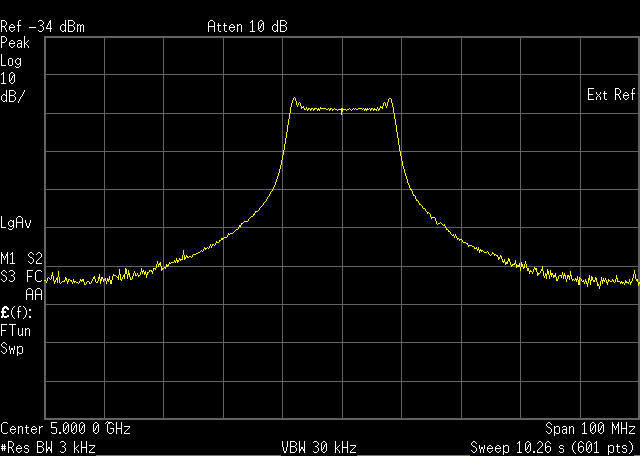
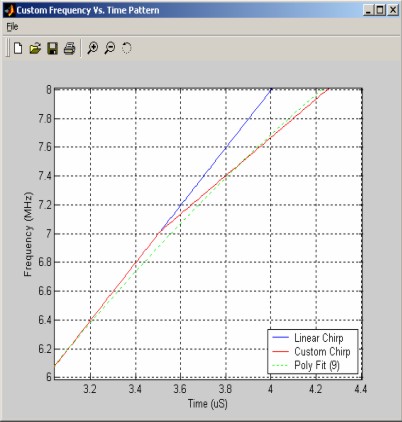
Figure 5 shows how using fewer coefficients results in a softening or filtering of the sharp transitions in the frequency pattern.

Figure 5 - Insufficient coefficients to follow desired frequency pattern

MatLab Scripts

function p = WobbulatingChirpCoeffs(n,sr,pw,pkdev)

% This function generates the polynomial coefficients

% for a linear chirp with sinusoidal wobulation on it.

% INPUT PARAMETERS:

% n - Number of coefficients desired

% sr - Arb Sample Rate (Hz)

% pw - Pulse Width (S)

% pkdev - Peak deviation of the linear chirp (Hz)

% OUTPUT PARAMETERS:

% p - Array of coefficients - x0, x1, x2, ...

% EXAMPLE:

% p = WobbulatingChirpCoeffs(19,100e6,10e-6,10e6);

s1 = .2*sin(.5*pi*[-1:2/999:1]); % Generate Sinusoidal waveform scaled by 20%

s2 = [-1:2/999:1]; % Generic slope for instantaneous frequency of a linear chirp

lc = s2*pkdev; % Instantaneous frequency for a linear chirp

y = s1 + s2; % add shapes together

y = y / max(y); % Normalize the shape

y = y*pkdev; % Scale for 10 MHz peak deviation

t = [1:length(y)]/sr; % time across pulse width

t = t - max(t)/2; % -pw/2 <= x <= pw/2

p1 = polyfit(t,y,n-1); % Determine coefficients using MatLab polyfit function.

p = p1(end:-1:1); % reverse order of coefficients x(n), x(n-1), ..., x1, x0 to x0, x1, ...

% Plot the Frequency Vs Time

showit = 1;

if (showit == 1)

z = polyval(p1,t); % Use polyval to generate custom frequency shape

t = t*1e6;

figure('Name','Custom Frequency Vs. Time Pattern','Number','Off');

plot(t,lc/1e6);

hold on;

plot(t,y/1e6,'color','red');

plot(t,z/1e6,':g');

hold off;

grid on;

legend('Linear Chirp', 'Custom Chirp',['Poly Fit (' int2str(n) ')'],4);

ylabel('Frequency (MHz)');

xlabel('Time (uS)');

end

function p = DualRateChirpCoeffs(n,sr,pw,pkdev)