Time Domain

Table of Contents

Time Domain allows you to view a device response as a function of time.

In this topic:

Note: Time Domain measurements are only available on FieldFox with Option 010.

See the App Note: Time Domain Analysis Using a Network Analyzer.

Overview

In normal operation, the FieldFox measures the characteristics of a test device as a function of frequency. With Time Domain (opt 010), the frequency information is used to calculate the inverse Fourier transform and display measurements with time as the horizontal display axis. The response values appear separated in time, allowing a different perspective of the test device performance and limitations.

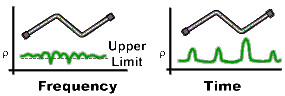
The graphic below compares the same cable reflection measurement data in both the frequency and time domain. The cable has two bends. Each bend creates a mismatch or change in the line impedance.

Time Domain and DTF Measurements

Time Domain and DTF (Distance to Fault) measurements are very similar. One of the main differences is that in Time Domain, the X-axis is displayed in Time (seconds). In CAT mode DTF measurements, the X-axis is displayed in distance. Another big difference is Time Domain includes the ability to 'gate' responses and prevent them from appearing in the Frequency Domain. DTF does not offer that ability. Which is the main reason why Time Domain is offered as an option.

How the FieldFox Measures in the Time Domain

Time domain transform mode simulates traditional Time-Domain Reflectometry (TDR), which launches an impulse or step signal into the test device and displays the reflected energy on the TDR screen. By analyzing the magnitude, duration, and shape of the reflected waveform, you can determine the nature of the impedance variation in the test device.

The FieldFox does not launch an actual incident impulse or step. Instead, a Fourier Transform algorithm is used to calculate time information from the frequency measurements. The following shows how this occurs.

A single frequency in the time domain appears as a sine wave. In the following graphic, as we add the fundamental frequency (F0), the first harmonic (2F0), and then the second harmonic (3F0), we can see a pulse  taking shape in the Sum waveform. If we were to add more frequency components, the pulse would become sharper and narrower. When the FieldFox sends discrete frequencies to the test device, it is in effect, sending individual spectral pieces of a pulse separately to stimulate the test device.

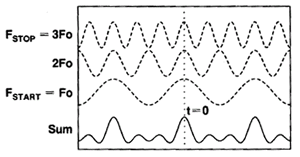
During an S11 reflection measurement, these incident signals reflect from the test device and are measured at the A receiver. This is when the time domain transform calculations are used to add the separate spectral pieces together.

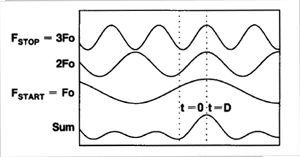
For example, consider a short length of cable terminated with an open. All of the power in the incident signal is reflected, and the reflections are 'in-phase' with the incident signal. Each frequency component is added together, and we see the same pattern as the simulated incident would have looked (above). The magnitude of the reflection is related to the impedance mismatch and the delay is proportional to the distance to the mismatch. The x-axis (time) scale is changed from the above graphic to better show the delay.

 

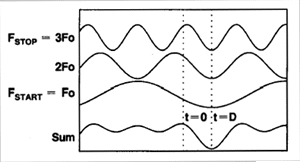
Alternately, the same cable terminated with a short also reflects all of the incident power, but with a phase shift of 180 degrees. As the frequency components from the reflection are added together, the sum appears as a negative impulse delayed in time.

Calibration for Time Domain

For simplicity, we have discussed incident signals reflecting off discontinuities in the test device. By far the most common network analyzer measurement to transform to time domain is a ratioed S11 measurement.  An S11 reflection measurement does not simply display the reflections measured at the A receiver - it displays the ratio (or difference) of the A receiver to the Reference receiver. In addition, the S11 measurement can also be calibrated to remove systematic errors from the ratioed measurement. This is critical in the time domain as the calibration reference plane (the point of calibration) becomes zero on the X-axis time scale. All time and distance data is presented in reference to this point. As a result, both magnitude and time data are calibrated and very accurate.

Although a time domain trace may be displayed, a calibration is always performed and applied to the frequency domain measurement which is not displayed.

Transmission Measurements

The most common type of measurement to transform is an S11 reflection measurement. However, useful information can be gained about a test device from a transformed S21 transmission measurement. The frequency components pass through the test device and are measured at the B receiver. If there is more than one path through the device, they would appear as various pulses separated in time.

For example, the following transmission measurement shows multiple paths of travel within a Surface Acoustic Wave (SAW) filter. The largest pulse (close to zero time) represents the propagation time of the shortest path through the device. It may not be the largest pulse or represent the desired path. Each subsequent pulse represents another possible path from input to output.

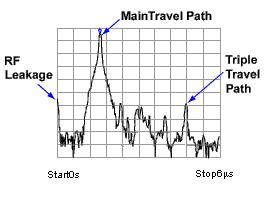
Triple travel is a term used to describe the reflected signal off the output, reflected again off the input, then finally reappearing at the output. This is best seen in a time domain S21 measurement.

Measurement Response Resolution

In the previous paragraphs, we have seen that using more frequency components causes the assembled waveform to show more detail. This is known as measurement response resolution, which is defined as the ability to distinguish between two closely spaced responses.

Note: Adjusting the transform time settings improves display resolution, but not measurement resolution.

The following graphic shows the effect of both a narrow and wide frequency span on the response resolution. The wider frequency span enables the analyzer to resolve the two connectors into separate, distinct responses.

Resolution Formula

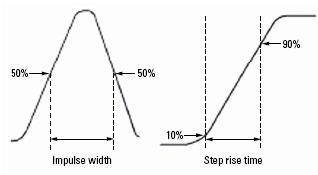
For responses of equal amplitude, the response resolution is equal to the 50% (−6 dB) points of the impulse width, or the step rise time which is defined as the 10 to 90% points as shown in the following image.

The following table shows the approximated relationship between the frequency span and the window selection on response resolution for responses of equal amplitude.

Window

Low-pass step

(10% to 90%)

Low-pass impulse

(50%)

Bandpass impulse

Minimum

0.45 / f span

0.60 / f span

1.20 / f span

Normal

0.99 / f span

0.98 / f span

1.95 / f span

Maximum

1.48 / f span

1.39 / f span

2.77 / f span

For example, using a 10 GHz wide frequency span and a normal window in Bandpass impulse mode, response resolution (in time) equals:

To calculate the physical separation (in distance) of the responses which can be resolved, multiply this value times the speed of light (c) and the relative velocity (Vf) of propagation in the actual transmission medium. In this case, Vf = 0.66 for polyethylene dielectric.

For reflection measurements, because of the 2-way travel time involved, this means that the minimum resolvable separation between discontinuities is half of this value or 19 mm.

Although a wider frequency span causes better measurement resolution, the measurement range becomes limited. Also, increasing the frequency range can cause a measurement calibration to become invalid. Be sure to adjust the frequency span BEFORE performing a calibration.

Measurement Range and Alias Responses

Measurement range is the length in time in which true time domain responses can be seen. The measurement range should be large enough to see the entire test device response without encountering a repetition (alias) of the response.  An alias response can hide a true time domain response.

To increase measurement range in both modes, change either of these settings:

Notes:

Alias Responses

An alias response is not a true device response. An alias response repeats because each time domain waveform has many periods and repeats with time (see How the FieldFox Measures in the Time Domain). Alias responses occur at time intervals that are equal to 1/ frequency step size.

The FieldFox adjusts the transform time settings so that you should only see one alias free range on either side (positive and negative) of zero time.  However, these settings are updated only when one of the toolbar settings are changed.

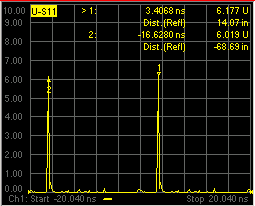
To determine if a response is true, put a marker on the response and change the frequency span. A true device response will not move in time. An alias response will move.

For example, in the above graphic, the marker 1 response occurs at 14.07 inches. When the frequency span is changed, this response remains at 14.07 inches. The marker 2 response moves.

Range Formula

You can calculate the alias-free measurement range (in meters) of the FieldFox using the following formula for TDR (reflection) measurements:  

Range (meters) = (1/Δf) x Vf x c

Where:

For example: For a measurement with 401 points and a span of 2.5 GHz, using a polyethylene cable (Vf = 0.66)

In this example, the range is 32 meters in physical length. To prevent the time domain responses from overlapping or aliasing, the test device must be 32 meters or less in physical length for a transmission measurement.

To calculate the one-way distance for a reflection measurement rather than round-trip distance, simply divide the length by 2.  In this case, the alias-free range would be 16 meters.

Gating

Perhaps the most beneficial feature of time domain transform is the Gating function. When viewing the time domain response of a device, the gating function can be used to "virtually" remove undesired responses.  You can then simultaneously view a frequency domain trace as if the undesired response did not exist.. This allows you to characterize devices without the effects of external devices such as connectors or adapters.

Note: When a discontinuity in a test device reflects energy, that energy will not reach subsequent discontinuities. This can "MASK", or hide, the true response which would have occurred if the previous discontinuity were not present. The FieldFox Gating feature does NOT compensate for this.

Example

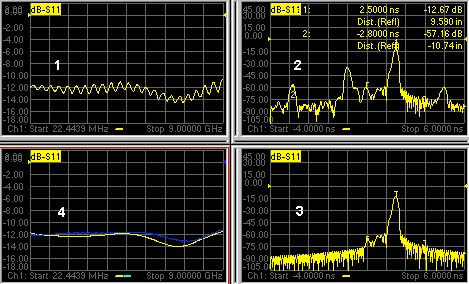
The following images show a practical example of how to use and perform gating. The test device is a 10 inch cable, then a 6 dB attenuator, terminated with a short. The following four discontinuities are evident in window 2, from left to right:

  1. A discontinuity in the test system cable which appears after calibration. It is identified by marker 2 at -10.74 inches (behind the reference plane).

  2. A discontinuity in the 10 inch device cable shortly after the reference plane.

  3. The largest discontinuity is the attenuator and short shown by marker 1 at -12.67 dB ( 6 dB loss in both forward and reverse direction).

  4. The last discontinuity is a re-reflection from the device cable.

We will gate IN the attenuator response. All other responses will be removed.

Window 1. Create original S11 frequency domain trace. Shows ripple from all of the reflections.

Window 2. Create a new S11 trace. Turn Transform ON.

Window 3. On the transformed trace, turn gating ON. Center the gate on the large discontinuity (2.500ns). Adjust gate span to completely cover the discontinuity. Select Bandpass gating type.

Window 4. On the original frequency measurement, turn Gating ON (Transform remains OFF). View the measurement without the effects of the two unwanted discontinuities. The blue trace is a measurement of the 6 dB attenuator with the unwanted discontinuities PHYSICALLY removed. The difference between the two traces in window 4 is the effect of "masking".

 

Gate Type  Defines the type of filtering that will be performed for the gating function. The gate start and stop flags on the display point toward the part of the trace you want to keep.

Gate Shape  Defines the filter characteristics of the gate function. Choose from Minimum, Normal, Wide, Maximum.

 

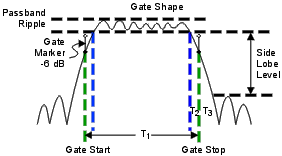
Gate Shape

Passband Ripple

Sidelobe Levels

Cutoff Time

Minimum Gate Span

Minimum

±0.1 dB

-48 dB

1.4/Freq Span

2.8/Freq Span

Normal

±0.1 dB

-68 dB

2.8/Freq Span

5.6/Freq Span

Wide

±0.1 dB

-57 dB

4.4/Freq Span

8.8/Freq Span

Maximum

±0.01 dB

-70 dB

12.7/Freq Span

25.4/Freq Span

Cutoff time The time between the stop time (-6 dB on the filter skirt) and the peak of the first sidelobe. The diagram below shows the overall gate shape and lists the characteristics for each gate shape.

Minimum gate span -- is twice the cutoff time. Each gate shape has a minimum recommended gate span for proper operation. This is a consequence of the finite cutoff rate of the gate. If you specify a gate span that is smaller that the minimum span, the response will show the following effects:

Window Settings

There are abrupt transitions in a frequency domain measurement at the start and stop frequencies, causing overshoot and ringing in a time domain response. The window feature is helpful in lessening the abruptness of the frequency domain transitions. This causes you to make a tradeoff in the time domain response. Choose between the following:

Last Modified:

4-Oct-2011

New topic