MIMO Characteristic Performance Analysis

Overview

The following characteristic performance results and analysis are for typical 2X2 MIMO systems comprised of E4438C ESG, N5182A/N5182B MXG, and N5172B EXG vector signal generators. They are valid for N7625C Signal Studio Pro for LTE/LTE-Advanced TDD 2024 Update 1.1 and also for other Signal Studio applications that support MIMO (for example, N7615C Signal Studio for 802.16 WiMAX and N7617C Signal Studio for 802.11 WLAN) since this performance is determined by the hardware platform and not the application-specific signals/waveforms.

This topic describes the MIMO performance for the following vector signal generators:

E4438C ESG
N5182A MXG, N5182B MXG, and N5172B EXG

E4438C ESG Performance

Test Overview

The following ESG MIMO configurations were tested:

A: ESGMIMO System without Baseband Timing Alignment or RF Phase Coherence

B: ESGMIMO System with Baseband Timing Alignment without RF Phase Coherence

C: ESGMIMO System with Baseband Timing Alignment and RF Phase Coherence

Two characteristic performance attributes were analyzed for each configuration. They are Phase Difference (between 2 ESG’s) vs. Time (at a fixed temperature) and Phase Difference vs. Temperature. The Keysight dual channel 89641S vector signal analyzer (VXI) was used to perform the measurements. The phase difference and other noise introduced by the 89641S have been removed from the measurement results, so the signal generator performance is accurately represented.

The following characteristic performance graphs are representative of the measurement results achieved on three sets of 2-ESG systems.

Test Results

Legend for pictures below:

Dark blue curve - measured phase difference.
Light blue curve - mean value of phase difference (every 20 points).
Pink line - Fitted line from the dark blue curve; shows the trend of the phase difference.

1. Results of configuration A: Two ESG MIMO system without common baseband clock and without RF phase coherency

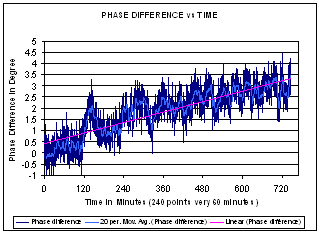
Figure 1-1 Phase difference over time for configuration A

At fixed room temperature of 26° C; Output Power = –10 dBm; Frequency = 2.412 GHz.

240 test points per 60 minutes.

From the plot, we can see 2.8 degrees phase change over 12 hours (pink line). The average peak-to-peak jitter of the phase difference is about 1.5 degrees (dark blue curve).

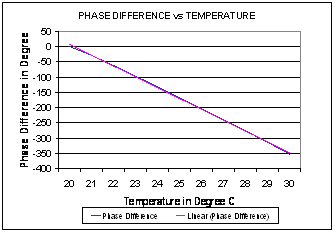
Figure 1-2 Phase difference over temperature for configuration A

Output Power = –10 dBm; Frequency = 2.412 GHz

From the plot, we can see about 35 degrees phase change per degree Celsius temperature change.

2. Results of configuration B: Two ESG MIMO system with common baseband clock and without RF phase coherency

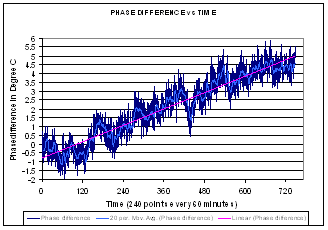
Figure 2-1 Phase difference over time for configuration B

At fixed room temperature of 26° C; Output Power = –10 dBm; Frequency = 2.412 GHz.

240 test points per 60 minutes.

From the plot, we can see 5.8 degrees phase change over 12 hours. The average peak-to-peak jitter of the phase difference is about 1.5 degrees.

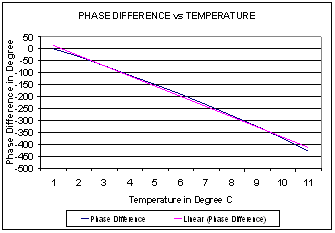
Figure 2-2 Phase difference over temperature for configuration B

Output Power = –10 dBm; Frequency = 2.412 GHz

From the plot, we can see about 40 degrees phase change per degree Celsius temperature change.

3. Results of configuration C: Two ESG MIMO system with common baseband clock and with RF phase coherency

Figure 3-1 Phase difference over time for configuration C

At fixed room temperature of 26° C; Output Power = –10 dBm; Frequency = 2.412 GHz.

240 test points per 60 minutes.

From the plot, we can see 0.17 degree phase change over 12 hours (pink line). The average peak to peak jitter of phase difference is about 0.15 degree (dark blue curve).

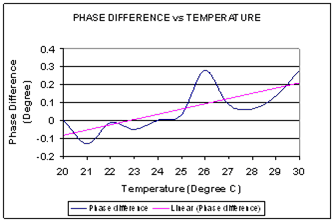
Figure 3-2 Phase difference over temperature for configuration C

Output Power = –10 dBm; Frequency = 2.412 GHz

From the plot, we can see about 0.03 degree phase change per degree Celsius temperature change.

Analysis for ESG Performance

As seen in the phase difference drift measurement results above, there are 2 main components in the phase difference drift:

1. Phase Difference A (referred to as PDA in this document) is the jitter or noise-like vibration shown in the phase difference curve, which is caused by phase noise.

2. Phase Difference B (referred to as PDB in this document) is the trend of the phase difference drift.

We use "Phase Difference” as the simplification of "Phase Difference Drift” in this document.

From the tests for all three cases, we can see that PDA dominates the measurement results. PDB is much smaller and its impact to most MIMO measurements is negligible. The analysis is:

If the environment temperature is stable (fixed), we can see that the phase difference drift is very slow, so only in a long-term continuous test could PDB be accumulated up to a value to be comparable with PDA. The continuous test means that there is no re-referencing in the test, i.e. no reset of the reference constellation etc. If the test is not continuous, PDB will be eliminated at re-referencing and will not be accumulated. Use configuration B, which has the fastest phase difference drift, as an example: it takes about (1.5/RMS_Factor )/(5.8/12) = 1.1 hour for PDB to be accumulated up to be comparable with PDA (1.5 degree peak-to-peak jitter) in a continuous test, where RMS_Factor is the factor to convert peak phase difference to RMS phase difference. This factor is 2.8, which is calculated from the test results. For configuration A and C, which have slower phase difference drifts, it takes even longer time.
If the environment temperature changes, the phase of one source may change relative to another source, even when both are locked to the same 10 MHz reference. The phase drift will continue over a long period as the source stabilizes at the new temperature. For example, if the environment temperature changes 5 degrees in 1 minute, it takes approximately 50 minutes for the source phase to settle.
But in ordinary measurements, such as the EVM measurement by the Keysight 89641S VSA, the data was captured within periods of several hundred milliseconds. The test reference (reference constellations) are reset at each capture (not continuous across captures). So, according the analysis above, the PDB doesn’t have time to accumulate in ordinary test (capture) periods and therefore it is very small in ordinary measurements. Thus it doesn't have any impact to the ordinary EVM and other MIMO measurements as compared to PDA under either the fixed or changing temperature conditions. In conclusion, PDA is the main factor that may impact your MIMO measurements, and PDB can be ignored.

Worst-case equivalent EVM for the phase difference values

If it is difficult for you to evaluate the impact of the phase difference value to your MIMO measurements, here we provide an approximate EVM equivalent to it which may help your evaluation. But the following conditions must be noted:

The values are worst case RMS EVM for the 2X2 MIMO setup with no fading case and an assumption is that there is no correction or optimization capability in the EVM measurement algorithm or the receiver. (Typically, either the receiver or the EVM calculation will do optimization to get the smallest residual EVM values.) Due to the pre-conditions above, the equivalent EVM values are the worst case values and may not be seen in real measurements.
The phase difference needs to be very small (<= 5 degrees) in order for us to take the approximations below. For all of the test results above, this assumption is met.

As concluded above, only PDA needs to be considered when making EVM measurements. As a result, the average peak-to-peak magnitude values of jitter are used for the phase difference values.

According to the first condition above (MIMO setup without fading, no correction), we can see the phase difference is an error angle in the constellation, which will introduce an EVM phase error without magnitude error. According to the second condition above, the EVM value can be approximated by the sine or tangent value of the phase difference, and then approximated to the phase difference itself (in radians). So we get the following formula:

EVM_rms (worst-case equivalent) = (PhaseDifference_pp(peak-to-peak-of-jitter) * PI/180) / (2*RMS_Factor)

where the factor 2 is the average factor for a 2x2 MIMO system which is used to put the EVM into two spatial streams to get the average EVM. RMS_Factor is the factor to convert peak phase difference to RMS phase difference. This factor is 2.8, which is calculated from the test results.

So we get

EVM_rms = 0.0031167* PhaseDifference_pp

This formula calculates the worst-case equivalent EVM for the phase difference impact to your MIMO measurement as below:

For configuration A and B: PhaseDifference_pp = 1.5 degree; worst-case equivalent EVM = 0.0047 (0.47%)
For configuration C: PhaseDifference_pp = 0.15 degree; worst-case equivalent EVM = 0.00047 (0.047%)

Conclusion

If your test requires phase coherency in your MIMO systems (e.g. you are working on beamforming in MIMO), you should choose configuration C.

Another benefit of configuration C is much smaller PDA, which results in much smaller worst case equivalent EVM. If you need to do high precision MIMO test, e.g. EVM with < 0.047% precision, etc., you may choose configuration C. But be aware that other components in your test setup, such as the receiver or analyzer, also contribute noise error that impacts the final precision of the measurements.

We don’t see significant differences between configuration B and configuration A in terms of phase difference drift. But configuration B will provide phase lock of the baseband clock between the ESGs. So, you should choose it if you need the locked phase (same phase or constant difference in phase) between the baseband clocks of the 2 or more ESGs.

N5182A MXG, N5182B MXG, and N5172B EXG Performance

You can use multiple N5182A signal generators in the same system, or you can use N5172B and N5182B signal generators in the same system. However, you cannot use a mixture of N5182A signal generators and N5172B or N5182B signal generators in the same system.

If you are using an N5172B or N5182B and one or more N5182A signal generators, you must configure the N5172B or N5182B as the Master. In addition, the N5182A slaves must be at the end of the instrument chain.

Test Overview

The following MXG/EXG MIMO configurations were tested:

A: MXG/EXG MIMO system with baseband timing alignment and without RF phase coherency

B: MXG/EXG MIMO system with baseband timing alignment and with RF phase coherency

Two characteristic performance attributes were analyzed. They are Phase Difference (between 2 MXG/EXG’s) vs. Time (at fixed temperature) and Phase Difference vs. Temperature. The Keysight dual channel 89641S vector signal analyzer (VXI) was used to perform the measurements. The phase difference and other noise introduced by the 89641S have been removed from the measurement results, so the signal generator performance is accurately represented.

The following characteristic performance graphs are representative of the measurement results achieved on two sets of 2-MXG/EXG systems.

Test Results

4. Results of configuration A: Two MXG/EXG MIMO system with baseband timing alignment and without RF phase coherency.
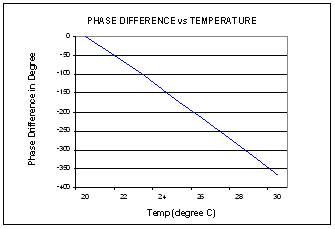
Figure 4-1 Phase difference over time for configuration A At fixed room temperature of 25° C; Output Power = –10 dBm; Frequency = 2.412 GHz. 1 test point per minute. From the plot, we can see the fastest trend change is 0.13 degrees Celsius per minute. The average peak-to-peak jitter of phase difference is about 1.5 degrees.	Figure 4-2 Phase difference over temperature for configuration A Output Power = –10 dBm; Frequency = 2.412 GHz From the plot, we can see about 37 degrees phase change per degree Celsius temperature change.

5. Results of configuration B: Two MXG/EXG MIMO system with baseband timing alignment and with RF phase coherency.
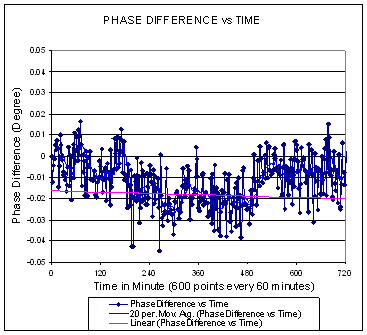
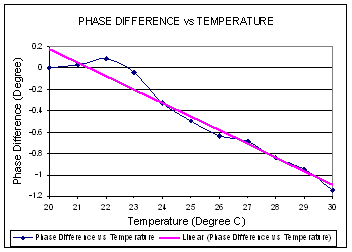
Figure 5-1 Phase difference over time for configuration B At fixed room temperature of 26° C; Output Power = –10 dBm; Frequency = 2.5 GHz. 600 test points per 60 minutes. From the plot, we can see a 0.05 degree phase change over 12 hours (pink line). The average peak-to-peak jitter of phase difference is about 0.06 degrees (dark blue curve).	Figure 5-2 Phase difference over temperature for configuration B Output Power = –10 dBm; Frequency = 2.412 GHz From the plot, we can see about 37 degrees phase change per degree Celsius temperature.